|
Different uses for voting
need different types of voting. |
 |
Hylland-Zeckhauser Points |
 |

The first rule here asks voters to lay out cards representing money. A more advanced budget-setting rule gives voters "influence points". But most voters want simpler ballots for easy voting, and simpler tally methods for maximum transparency.
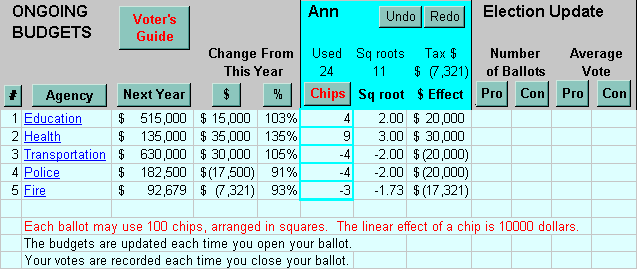
Square Root VotingA way to merely discourage exaggerated votes is to "tax" big votes more than small ones. There is little tax if you place just one row of cards across the width of the column. If you add a second row, you must stack them two deep; a third row, three deep. The depth is a tax. If you are willing to pay it, you can afford a few large votes -- but you lose more influence over other budgets.( It is easier if we require the voter to double only the second row, or any part of a second row, leaving the first row one card deep. This does not keep Hylland and Zeckhauser's "square-root" rule for the voters grant as a whole.) This gives voters more flexibility than they have using preset cards sizes. But moving cards is harder. Every time a rep removes a row of her cards from the middle of a column, the cards above must slide down to fill the gap. This can be tedious so it is practical only for small groups. Large groups can use computer-based ballots that immediately update the tally. Click the picture below to download a working prototype. What defines this fair-share rule is the length of the cards compared to the length of the columns. If each column is as long as 50 cards, then 50 voters can fill a column without paying any tax. This number is not a threshold nor quota because a lack of 50 cards does not eliminate the agency. It merely reduces the budget. Nothing is gained by breaking an agency into many small agencies with separate, narrow columns. 1. A voting table has empty columns for agency budgets.
If the quota is 50%, then each rep gets enough cards to fill half a row for each agency. If all did that, funding would be unchanged from last year. But someone might want a change. And someone else might counter it. A voter may fill 1 row of a budget with no tax. But to fill 2 rows, he must make each row 2 cards deep; for 3 rows, 3 cards deep stacked on the table. The depth is the tax for a big vote. Only the square root of a vote counts. Say a legislature with 100 seats sets its quota at 50. (A smaller group can maintain the funding for their favorite agency if they are willing to pay the tax.) The cards are about one inch square -- a size that is easy to handle. The voting table is simply a 4 by 8 foot sheet of plywood with columns running up the long axis. The first 4 feet of each column represents the top 10% of last year's budget. The next 4 feet represents an increase of 10%. Bigger cards or shorter columns would make a quota lower. If it is usual for some budgets to rise or fall by more than 10% we can start with columns representing more than 10% of each department's budget. The larger this figure, the greater the majority's advantage. Starting at 90%, a minority with enough members to half fill a favorite column provides 95% funding; starting at 80% it provides only 90% funding. Starting at 0% they get only 50% funding and the agency would need help from the majority which could effectively set the budget at 80%, 70% or any amount they want above 50% of last year's. Thus budget cards could let large parties undercut or negate a small minority's votes by simply removing votes for an agency if they feel the minority's votes have raised its budget too high. This undercutting leads to a winner-take-all rule. The definitions of "large" and "small" are set by the quota. If a majority could not negate a small minority votes, then the minority could surprise an agency with a sudden change in funding. That could destabilize a government.
(If budgets are not stable after a time, a simple majority may end the voting. It should stop smoothly, not abruptly. The chair might announce In the next [10 minutes] each rep may move only $100... And then: In the next [10 minutes] each rep may move only $30... and finally $10...) Bylaws may require a majority vote to enact the final result. This prevents a last-second surprise by one group from cutting or funding a department. If the result is rejected, voting continues for a set time. StrategiesA rep could give 36 cards to a favorite item and push it up eight. Or she could join a dozen other reps, give three cards to each partner's favorite and push each up by two. The total effect of 12 times 2 is 24, much bigger than eight.Few voters will place large votes and pay the tax when they begin with so few cards compared to the number and widths of columns. Vote trading is a much more attractive tactic. A voter who uses many large votes restores little to the overall budget. What should happen to the unspent money? A pure tax is immediately given to all the other voters. The council may raise all budgets by the fraction needed to consume the unspent money if the amount is small. Or, if it is large, they may send it to a second vote a few days later or add it to the next allocation period, to endowment, to debt repayment, to projects, or to a combination of these. If it reduces the need for revenue (taxes or dues) in the next fiscal period, voters who want lower taxes may have an advantage when it comes to placing large squares. A column for tax relief or increase would allow a rep to influence the overall budget. And if she adds to tax relief, she must take away from another budget. But what width should this column have? A Democratic SolutionThe rule for fair agency budgets developed from a more majoritarian system which its inventors, Annund Hylland and Richard Zeckhauser, called Influence Points, IP. Here is a simple version using cards for influence points.Council members use "balloons" and "weights" to raise and lower budgets. Their balloons and weights are symbolized by cards. As in any honest game, reps "must lay their cards on the table." This particular table forms a bar chart, and each agency has a column where reps may lay cards. A flag marks an agency's initial funding which is set by last year's budget. Reps put balloons above an item's flag to raise it, and weights below to lower it. The item's budget at any time is half way between the highest balloon and the lowest weight. Reps move cards repeatedly to cause or counter budget changes. A rep's cards might total 100 units in area. A single card, 10 by 10 square, can lift or sink 1 budget dramatically. Or a rep might move 4 budgets with 4 cards, each 5 by 5 square. A rep may use any combination of square cards that adds up to an area of 100. The committee's rules may require each rep to balance her balloons and weights. Otherwise, a rep who wants to increase services and taxes (or dues) gives out balloons and one who wants to reduce taxes and services gives out weights. Voting ends when budgets are stable. That is when no budget changes more than [2] % over [20] minutes. This is an equilibrium. If budgets are not stable after a time, a simple majority may end the voting. It should stop smoothly, not abruptly. The chair might announce "In the next [10 minutes] each rep may move only [5] squares." And then: "In the next [10 minutes] each rep may move only [3] squares." ...and finally 1 square. (These descending numbers are the differences between arithmetic squares: 9-4=5, 4-1=3. This lets a rep cut a large vote down to the next convenient size.) Bylaws may require a majority vote to enact the final result. This prevents a last-second minority surprise from cutting or funding a department. If the result is rejected, voting continues for a set time. Each card shows the rep's name so her final votes can be totaled and published. (Cards also may be given pictures from rockets to ship wrecks.) The TrickSo voting is easy; reps can see and feel the budgets rising and falling. There has to be a catch right? Right. It is widely known that the best strategy for simple point voting is to dump all your points on your favorite. This is bad for decision making. It is not an accurate vote. It doesn't tell the public or the vote-counting rule how you rate all the other items. It rewards exaggeration.The IP trick: Only the square root of the vote counts. Reps don't need to calculate square roots; a square card shows both the rep's political cost and the agency's budgetary effect of a vote. The cost is the area; the effect is the length. Someone may put 4 points on 25 items and push them 2 each, 50 total. Or she might put 4 points on 12 items and 25 points on 2 items, for a total push of 34. The group may want to limit the number of cards a voter may place on 1 item. Each rep might get 1 by 1 cards to make into squares of any size; no large cards are needed. The number of cards for a rep might equal 2 times the number of items; experience will show the best ratio for each council. The length of a card may represent $5 on a table of $100 budgets, or $10,000 where budgets are in the millions. Criticisms of H-Z Influence PointsThe dynamics of IP are similar to those under Fair-share Agency Budgets.But unlike fair-share rules for projects and budgets, IP cannot guarantee power for minority reps: A "ruling majority" can counter each vote cast by a minority. But when there is no fixed majority all reps have some power, making the budgets change as the reps do and accurately linking the election to the budget. Such an "open majority" is most likely in an ensemble council. "Subdividing" a department to list it as several agencies lets a supporter place 1 card in each new column -- for maximum influence with minimum cards. But opponents can do the same with negative cards, so there is no net advantage -- if the factions are equal in size. But splitting departments helps the larger faction. Say a majority has 36 cards or influence points to give to Dept. B while their opposition has 16 points to place against B. The square root of 36 minus the square root of 16 is 6 - 4 = 2. Now say the majority divides the department into 4 line items. They give 9 points to each and the opponents put 4 against each. The calculation is now 4 × the square root of 9 minus 4 times the square root of 4. 4 × 3 - 4 × 2 = 12-8 = 4. This lets the majority double its power. The fair-share version reduces that incentive by making the tax rate a function of the percentage change. Say Dept. B starts from 100 units and the majority adds 36; that is 36% [36/100]. If they divide it into 4 line items each starting with 25 units and then add 9 to each, that too is 36% [9/25] and each still gets the tax rate for a change of 36%. Multiplying that tax rate by the item's starting budget(s) makes the rule fair to large and small agencies. [ But now the votes vary from 0 to about 2 and the square root function is nearly constant over that limited range, perhaps not as progressive as the tax must be to prevent dumping. So Budget Points might use exponential growth functions.] Under IP there is an advantage in sub-dividing agencies if people place more cards for agencies than against. Most reps hesitate to place cards against another's fiefdom. Say for example, you chair the transportation committee so you watch that column closely. You notice when I place cards against the transportation budget and you're likely to take a dim view of the action -- which makes me reluctant to do it. The FIP rule therefore requires each rep to balance positive and negative changes. A column for tax relief or increase still would allow a rep to influence the overall budget. And if she adds money to tax relief, she must take money away from another budget. A rep needs to see the current budgets and repeatedly move her cards. A network-based ballot like the one pictured below is a good method. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

|

|
|

 Accurate Democracy
Accurate Democracy