Data on Manipulability

The voting rules discussed here were defined on the Other Rules page in the chapter about single-winner elections.

In 2010, James Green-Armytage at the University of California Santa Barbara published Strategic Voting and Nomination.

“Abstract: Using computer simulations based on three separate data generating processes, I estimate the fraction of elections in which sincere voting will be a core equilibrium given each of eight single-winner voting rules. Additionally, I determine how often each voting rule is vulnerable to simple voting strategies such as ‘burying’ and ‘compromising’, and how often each voting rule gives an incentive for non-winning candidates to enter or leave races. I find that Hare is least vulnerable to strategic voting in general, whereas Borda, Coombs, approval, and range are most vulnerable. I find that plurality is most vulnerable to compromising and strategic exit, and that Borda is most vulnerable to strategic entry. I support my key results with analytical proofs.”

This confirms and extends the findings of John Chamberlin et al at the University of Michigan, and of Samuel Merrill III at Wilkes University. The key tables from those earlier studies are shown below with the authors' permissions.

Punishing the leading candidate with last-place votes

In contrast, punishing the leading candidate with a last-place vote cannot help the voter's first choice to win under Condorcet's rule. The voter already ranks his favorite as number one. So an insincere ballot cannot increase the number of voters who rank his favorite, B, ahead of the main rival, A.

But the punishing vote might decrease the chance that A could win by Condorcet's rule, because the insincere voter might be helping another candidate, C, (whom he would rank below both A and B on a sincere ballot) to beat the original leader. This may make C win by Condorcet's rule or it may create a voting cycle. In fact, even if most voters would honestly rank C last, insincere ballots can sometimes make her a Condorcet winner. Systems that reward punishing votes are less likely to find true Condorcet winners.

I have adapted this example from one Merrill (on page 66) used to prove that Condorcet-completion rules do not necessarily elect true Condorcet winners when voters have polling information and then vote strategically. Black's, Copeland's, Dodgson's, and Kemeny's Condorcet-completion rules all fail this real-world test.

	Ballot	  4	  4	  1
	ranks	voters	voters	voter
	1st	  A	  B	  C
	2nd	  B	  A	  A
	3rd	  C	  C	  B

Pairwise comparisons A gets 5 votes to 4 against B etc.

		A	B	C  
	A wins	 -	5:4	8:1
	B	4:5	 -	8:1
	C	1:8	1:8	 -

From this pre-election survey, the major voting rules give a unanimous result:

			   Candidates	
	Voting rule	A 	B 	C
	Agenda     	v			
	Plurality	4	4		tie
	Runoff    	v		
	Approval 1	4	4	1	tie
	Approval 2	9	8	1
	Black     	v		
	Borda     	13	12	2
	Coombs    	v		X
	Copeland  	2	0	-2
	C-IRV  		v		
	Dodgson    	0	-1	-4
	M-IRV   	v		X
	Kemeny   	0	-1	-8
	Minimax  	+11	-11	-78
	Std-score[2]	4	3	-7

	(Con) = a Condorcet-completion system.
	X = an eliminated candidate.
	v = victory.

Now all voters know that A leads the race. Voters opposed to A can "punish" her with last-place votes to decrease her score relative to the other candidates. In Example 1 b, supporters of B decide to vote strategically.

b) Strategic Voting by B's party

Interest groups' ballots

	Ballot	  4	  4	1  
	ranks	voters	voters	voter
	1st	  A	  B	  C
	2nd	  B	  C	  A
	3rd	  C	  A	  B

Pairwise comparisons. A gets 5 votes to 4 against B etc.

	   A	  B	C
	A  -	  5:4	4:5
	B  4:5	  -	8:1
	C  5:4	  1:8	-

A bests B who bests C who bests A. This voting cycle makes the Condorcet-completion rules use a second rule to decide their winners. Whether or not they are based on Condorcet, most rules are easily defeated by punishing votes. Our rules produce these results for the final election:

			   Candidates	
	Voting rule	A 	B 	C
	Approval 1	4	4	1	tie
	Approval 2	5	8	5
	Black    		v	
	Borda    	9	12	6 
	Coombs    	X	v	X
	Copeland	0	0	0	tie
	C-IRV  		v		X
	Dodgson   	-1	-1	-4	tie
	M-IRV    	v		X
	Kemeny    	-2	-2	-5	tie
	Minimax %	-11	-11	-77	tie
	Std-score	0	3	-3

By voting strategically, B's supporters would win or tie the election according to most voting rules. C's supporters also can vote insincerely against A. But they would only help B not C. A's supporters may try to counter B's strategy by punishing B. In that case all of these rules would choose C; the least-liked candidate would be the apparent Condorcet winner! The important point is that A would not need to counter B's strategy in this case under C-IRV, or M-IRV.[2]

Frequency of manipulable elections

	Year     	1976	1978	1979	1980	1981
	# of voters	11560	15285	13535	15449	14223

The researchers reported:

“The most striking result is the difference between the manipulability of the Hare system and the other systems. Because the Hare system considers only 'current' first preferences, it appears to be extremely difficult to manipulate. To be successful, a coalition must usually throw enough support to losing candidates to eliminate the sincere winner (the winner when no preferences are misrepresented) at an early stage, but still leave an agreed upon candidate with sufficient first-place strength to win. This turns out to be quite difficult to do.

“One other factor also distinguishes the Hare system from the other[s]. The strategy by which Hare can be manipulated, on the occasions when this is possible, is quite complicated in comparison with the strategies for the other methods.” (Chamberlin, Cohen, and Coombs)

The authors contrast those strategies for 2 pages. As they and Merrill imply, the first preference is the rank most likely to be sincere on each ballot. The manipulability of the three Condorcet-completion rules (Kemeny, Minimax, and Black) proves that in each election a group of voters could create a voting cycle and also change a count such as the Borda used by Black's rule. Still, page 6 shows the need to create a cycle makes C-IRV even harder to manipulate than M-IRV because it increases the number of voters who must be organized into a conspiracy.

Tideman's findings reportedly agree with these.(Merrill, page 70) He used data from "thermometer" surveys of voter opinions about the candidates for the 1972 and 1976 presidential nominations. It is worth noting that he found Dodgson's Condorcet-completion rule about as resistant to manipulation as Hare's (M-IRV) rule. But to manipulate Dodgson's rule needs less information than IRV requires about other voters' preference lists. So those who want to manipulate Dodgson can plan and coax voters into a simple strategy.

Irrelevant alternatives

This political trick is fairly simple and common.

Table 4. Violations of Independence of Irrelevant Alternatives
Spatial model of 200 voters and 5 candidates repeated in 1,000 elections
from Merrill, page 98

	Voting system		Violation %
	Plurality		   19
	Runoff  		   10
	Approval		   9
	Borda   		   7
	Hare (M-IRV)		   6
	Coombs    		   1
	Black (CW/Borda)	   0.1

	[ C-IRV 	   0.1  estimated III ]

Case Study: Republicans Split Northern and Southern Democrats.

Let's see what would have happened under different voting procedures. Here are the approximate sizes and preferences of the three voting blocks.

Example 2.
Republicans, Northern & Southern Democrats

Ballot	161 Northern	80 Southern	    160
ranks	 Democrats	 Democrats	Republicans
1st 	Amended		Bill		No bill
2nd	Bill		No bill		Amended
3rd	No bill		Amended		Bill	


	Pairwise comparisons
		Amended	   Bill  
	Bill	80:321	   -
	No bill	240:161	   160:241
 

This is a voting cycle. The amended bill beats the plain bill by 321 votes to 80 votes. The plain bill beats no bill by 241 votes to 160. And no bill beats the amended bill 240 to 161.     A > B > N > A.

Should they pass a bill to increase funding and fight segregation? If the House votes first on funding then on desegregation both would pass; if the Republicans vote for the desegregation amendment they proposed. But most parliamentary procedures require voting on the amendment before the bill. So the House would pass the amendment and then defeat the bill - as actually happened. This case follows Duncan Black's rule of thumb as cited by Straffin, "...the later you bring up your favored alternative, the better chance it has of winning"(page 20) Here Bill which could beat No bill was itself beaten in the previous round by Amended bill.

They get the same result, nothing, from the C-IRV and M-IRV voting systems as noted below. Keep in mind that without the amendment, the plain Bill would have passed by 241 Democratic votes to 160 Republican votes.

				Options
	Voting		Amended	Plain 	No 
	Rule		Bill	Bill 	bill
	Agenda			v
	Plurality	161	80	160
	Runoff			v
	Approve of 1	161	80	160
	Approve of 2	321	241	240
	Black     	v		
	Borda     	482	321	400
	Chamberlin	X		v
	Coombs    	v		X
	Copeland	0	0	0	tie
	C-IRV		X	v
	Dodgson    	-40	-121	-41
	M-IRV     	X	v
	Kemeny    	-40	-121	-41
	Minimax % 	-19.7	-60	-20.2

If the Northern Democrats out-number the Republicans then Amended bill would win by most rules. Under Copeland all options would tie. Under agenda, M-IRV, and C-IRV No bill would win. We would say C-IRV was manipulated by an irrelevant alternative because the new alternative did not win, yet reversed the order of the original two options.

The Republicans might argue that they exposed the fact that some of the school funds would have gone to support racist school districts which most voters did not approve of and did not want to pay taxes for. Because of this new issue dimension, previously unconsidered, C-IRV reverses its result. If the Republicans had added an amendment to set funding higher or lower than the Democrat's bill, then the C-IRV result would not be reversed. No bill would still be defeated - by either the original Bill or the Amended bill's funding amount. The amendment certainly was not an irrelevant issue; but strictly speaking it was an irrelevant alternative.

	     2 Issue Dimensions     
		Funding $	Desegregation
	Yes	241		321 (maybe)
	No	160		80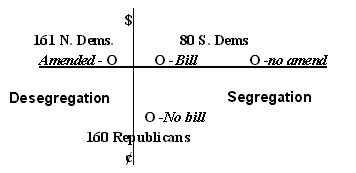

If the Republicans outnumber the Northern Democrats, that switch of one vote changes the result to No bill under most voting systems. If the Republicans rank the desegregation Amended bill last, and raise the plain Bill to second place, then the plain Bill would beat each of the other options in one-on-one contests and win under most voting systems. No bill could still win only under agenda and Hare.

The Republicans in this case used several manipulation techniques. First they introduced an amendment that some theorists might consider an irrelevant alternative. It created a voting cycle. Then they probably voted insincerely to punish the leading option. No one can prove insincere votes but many of these same Republicans often voted against desegregation so I doubt they sincerely preferred the Amended bill over the plain Bill.

I give this negative example of C-IRV last to impress upon readers that no decisive, non-dictatorial voting system can guarantee complete resistance to manipulation in all situations. C-IRV is most subject to manipulation in committee voting. Dennis Mueller writes in a section titled "Cycling", "Thus it would seem that when committees are free to amend the issues proposed, cycles must be an ever present danger." (page 64) If the amendments create a cycle, then C-IRV starts to eliminate proposals. It is hard to manipulate that process, but it is possible.

Deleting less popular candidates can change the winner also. This test uses real-world ballots to measure a voting system's vulnerability to changes in the slate's minor candidates.

Table 5. Violations of Subset Rationality
data from Chamberlin, Cohen, and Coombs (1984)
Number of violations when X is reduced from 5 candidates to 2, 3, or 4.

Voting		2		3		4	
system	  Candidates	  Candidates	  Candidates	      Total
Plurality	5		7		2		14
Borda   	2		2		1		5
Hare (M-IRV)	2		2		0		4
Coombs   	0		0		1		1
Approve 2	1		17		1		19
Approve 3	3		6		5		14
[ Condorcet	0		0		0		0 R.L.]

The authors note that "Violations of this subset rationality condition when a single candidate is omitted seem most serious..." Hare was the only system with no violations when a single candidate was omitted.

There were no cycles in the real-life elections and polls studied by these authors. Other research also finds cycles are not common. “It is notable that both data sets have voting cycles — the 913 ANES surveys have 4 cycles (0.44 percent), and the 20,087 ERS [Electoral Reform Society] elections have 476 cycles (2.37 percent). However, there are only 101 voting cycles (1.45 percent) among the 6,794 ERS elections with 21 or more voters, and only 6 voting cycles (0.68 percent) among the 883 ERS elections with 350 and more voters. Thus the frequency of voting cycles falls fairly quickly as the number of voters increases.” The Structure of the Election-Generating Universe by T. Nicolaus Tideman and Florenz Plassmann; 2010

Sensitivity to incomplete ballots

To better understand the effects of incomplete ballots, we need a study similar Chamberlin and Cohen's on the deletion of candidates, shown in Table 5. For now I shall re-use some of their published results to estimate the sensitivity to incomplete ballots for five voting systems. Tables 2a and 2b in their article showed how five election rules ranked all candidates, from winner to last-place loser. Table 2a showed their results when they filled the incomplete ballots uniformly - giving no favor to any candidate. The researchers state: "This corresponds to the assumption that voters are indifferent to candidates whom they do not rank." Table 2b gave their results when they filled the ballots proportionally - making the artificially-completed ballots resemble voter-completed ballots with the same initial preferences. This method corresponds to an assumption that voters omitted candidates because they lacked sufficient knowledge, and that if these voters had the knowledge necessary to complete their ballots they would have done so with the same preferences as those on the similar but completed ballots.

If a voting system showed many differences between those two tables, then it is very sensitive to how the incomplete ballots are filled - and probably sensitive to the use or deletion of incomplete ballots. Table 6 shows the number of differences, in winners and complete social rankings, between Chamberlin, and Cohen's Tables 2a and 2b.
 

Table 6. Sensitivity to Methods of Filling Incomplete Ballots
from data of Chamberlin and Cohen (1978)

Most of the systems tested by Chamberlin and Cohen sometimes picked a different winner depending on which completion method they used. A change of winners more seriously effects us than a change further down the collective ordering. So I tentatively rank the voting systems' sensitivity to incomplete ballots as: plurality, approve 2, (approve 3, Borda, Hare), and Coombs. This list seems reasonable based on how the systems select winners. Plurality always picked the same winner, runner-up and so on, no matter which completion method the researchers used. It uses only the first choice; so whatever they filled in below made no difference. Coombs eliminates the candidate with the most last-place votes; so how they filled the bottom of the ballots made a big difference.

Incomplete ballots cause no greater problem for C-IRV than for most multi-candidate systems. In a later section I will argue that faulty ballots are least likely to occur under C-IRV.

To sum-up this section comparing C-IRV with the other voting rules: 1) C-IRV probably is no more sensitive to incomplete ballots. C-IRV has the highest possible efficiency at picking the candidate with broad support and it has a very high social utility efficiency. 3) Most importantly, C-IRV resists manipulation very well and always elects a candidate close to the center. So in competitive political situations its winners probably will have higher Condorcet and utility efficiencies than any other voting system's. It induces the sincere ballots needed by any voting system for electing utility maximizing and Condorcet candidates and finding the greatest happiness for the greatest number of voters.

Endnotes

1) “...all voting systems permit manipulation, as was shown by Gibbard (1973) and Satterthwaite (1975). Thus, the practical questions for social choice theory to answer are the extent to which different systems encourage strategic calculations in voting, their effects on the nature and perceived legitimacy of the outcome, and their implications for political stability.” (Merrill, page xvii)

2) Standard scores of -1, 0, and 1 are used for simplicity. Of course, the system allows any value between the extremes on a continuous scale.

3) Merrill states of the Hare system, “There is also no incentive, as there is under the Borda count, for a voter to move the chief rival of his favorite to the bottom of his preference order. As long as his favorite remains in the race, lower preferences are not counted. If his favorite is eliminated, there is no motivation for the voter to try to punish his former chief rival.” (page 65)

4) Other manipulations include changing the sequence of preferences as the third voter did on page vii. That particular change, not voting for his first choice, is called decapitation and is most common under single-vote plurality. (Please see figure 6 on page 25.) Many other rules reward bullet voting or plunking: voting only for one's first choice.

5) This concerns the frequency of manipulable elections as found in simulations and practice. It does not contradict the theoretical proofs by Gibbard and Satterthwaite that any possible voting system is manipulable to some degree.

6) In 98% of Merrill's spatial-model elections there was no voting cycle, so Black's rule used the Condorcet criterion — whose results did not change due to irrelevant alternatives. In the remaining 2% of elections Black used Borda's rule — which was vulnerable to irrelevant alternatives in 7% of these elections. 2% x Borda's 7% manipulability = 0.14% which rounds to 0.1%. This was the number Merrill reported for Black, but his number came from simulation of Black. He did not infer it from simulations of Condorcet and Borda. C-IRV's score also would be zero for 98% of the elections. Add 2% of Hare's score for a total of 0.12%. These estimates assume that violations are equally common in elections with and without cycles.

 More References 

James Green-Armytage, "Four Condorcet-Hare Hybrid Methods for single-winner elections"; Voting Matters; 2011.

James Green-Armytage, "Strategic Voting and Nomination"; Social Choice and Welfare; 2014

James Green-Armytage, T. Nicolaus Tideman and Rafael Cosman, "Statistical Evaluation of Voting Rules"; 2014

Nicolaus Tideman; Collective Decisions and Voting; (Ashgate Publishing Ltd., Hampshire, England; 2006) page 232.