Fair-Share Ballots II

Advanced-Ballot Calculation

My ballot can offer money to each of my top choices by calculations that depend on whether I choose to rank, grade or score the projects.  If I score my "joy in project B" at 200 and another project of equal cost at 100, the ballot gives twice as many votes to project B.  If I rank or grade the projects, I may choose a line such as this one and make the vote for an item its average height under this line.
[ Move the ruler from the two-vote line to bisect the top of each column.]

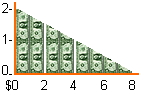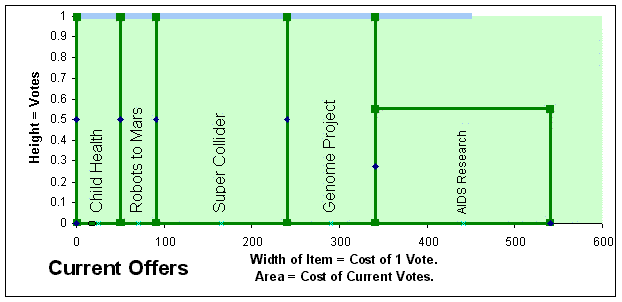
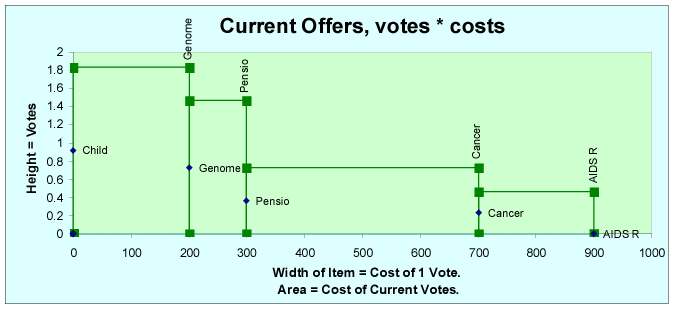
( This option automatically gives more than one vote to my first dollar of suggested budgets  [Point to the first dollar of the first choice.]  and less than one to my share's last dollar of suggested budgets.  [Point to the last dollar of the last choice.]  Each of my favorite's automatically gets a vote in between this maximum and this minimum.  So the average dollar of these suggested budgets gets one vote.)

Charts of Offers

The charts below were made by an Excel ballot for advanced Movable Money Votes.  Each chart graphs one ballot's current "offers".  The voter's favorite items each have a box on his graph.  A box's height shows the number of votes for that item.  A box's width shows the cost of 1 offer (and 1 vote).  So the area in a box shows how much money the ballot currently offers the item; that is the item's number of votes times its cost for each vote.

Graph 1: The ballot below is offering one vote each to as many items as it can afford.  The line starts at 1 vote, where it intercepts the vertical Y axis.  The angle or slope of the line is 0 times X.
   horizontal straight line = (0 × X)  + 1  

Often a ballot runs out of money in the middle of an item, so it gives that item a "partial vote".  This ballot can afford only a partial vote for Aids Research.

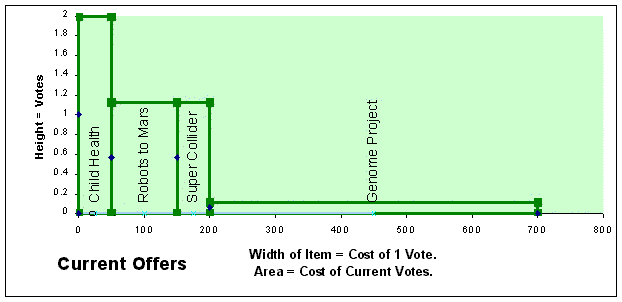
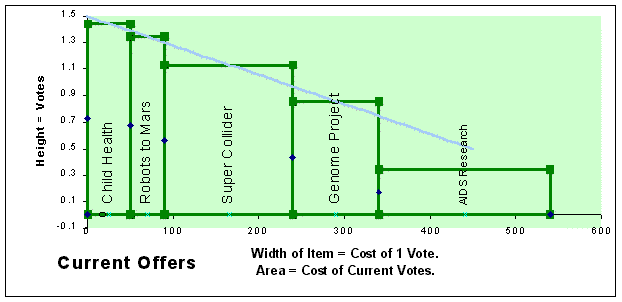
Graph 2: This next ballot helps the favorite item more than the second or third choice.  But it has no more spending power than the ballot above because both give a total of 1 vote to 1 share of money.  The area under both lines is the same.  All five of these graphs have an area equal to 1 vote (on the Y axis) times 1 share of money (on the X axis.)    straight line = (-1 × X) + 1.5

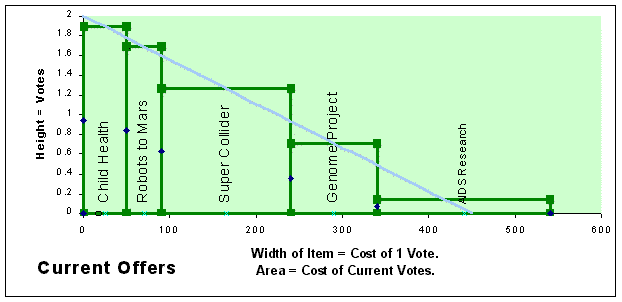
Graph 3: The ballot below helps the favorite item more than the second favorite.  It gives little help to the last item on the right.    straight line = (-2 × X) + 2
The steepest predefined curve usually gives the best result for the voter's top choices.

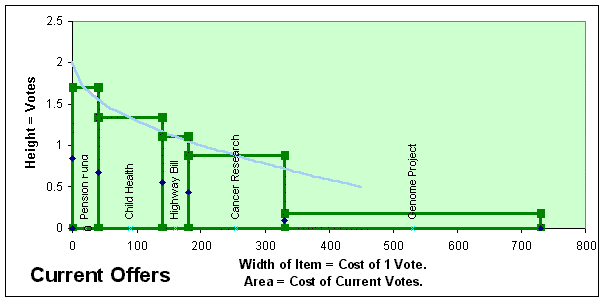
Graph 4: The funding curve below gives almost 2 votes to the first choice yet still tries to give a half vote to the last choice within 1 share ($475.).  In this case the last item is too costly, so it gets only a partial vote.    curved line = (-1.5 × X ^ (1/2) ) + 2

A voter may score items instead of grading or ranking them.  His scores tell the tally "I like B twice as much as C."  Such ratios let the tally construct his personal "utility curve".  The tally uses his curve to apportion his share of funding.  It does not compare or aggregate his scores with scores from other voters.

Graph 5:: voter's funding defined by scores

Rewarding Sincere Scores

The funding graph on the left has a heavy black box representing money for one or two favorites and an empty white space for all other preferences.  Contrast that with the graph on the right, a gradient from black to white under a curve.

So scoring might give a rep only a false and temporary sense of freedom of expression.  Her choice might not be any score between 0 and 2 votes; it might be just two scores, either 0 or 2 votes.  (Graded and ranked ballots use pre-defined curves, like the one on the right, to create more self-expression.)

Here are three forms of the black-and- white strategy and ways to prevent them.
    1) The first trick a wily rep often tries is to give all her weight to her first choice.  This would defeat our desire to see that each item win substantial support from a significant number of voters. -- So we set a maximum vote, usually two.
    2) The second strategy she tries is to give the maximum vote to every favorite.  So we make each ballot's average vote equal one.  If all high choices have the same score they will each get just one vote.
[Merrill's Standard Score takes this further by adjusting a ballot's scores so they average one and so they spread out to fit a normal bell curve.  This pushes up a small top choice; it can get up to 3 votes but only if the voter scores larger items close to zero.]
    3) The third strategy she tries is scoring items 1, 10, 100, 1000, and so on multiplying by ten to ensure that the current top item always gets the maximum vote allowed.  This is prevented by setting a limited range of scores, most often 0 to 100 or 0 to 1000.

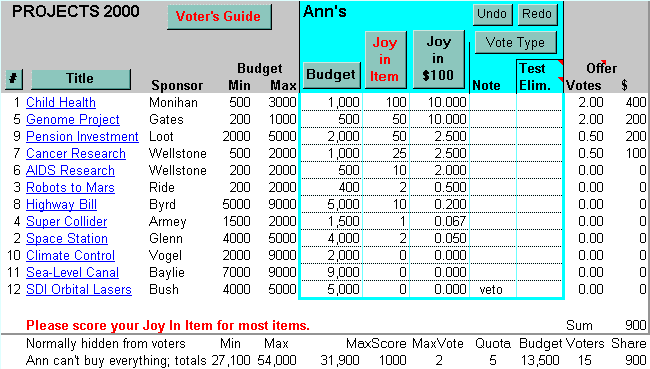
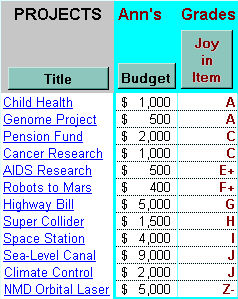
The ballot below prevents these strategies and so encourages sincere ballots to give voters equal power and to find common goods.

Try a Ballot

The simplest way to vote is by putting projects in categories which say, "These are grade A projects; these are grade C and those are grade Z." The most precise way to vote is to give scores which say, "This one is worth 1.25 times as much as that one." This ballot allows voters to switch between simplicity and precision.

A voter rates her joy in each item.  The ballot offers money first to the most cost-effective items, those with the highest "Joy in $100".  When a voter rates a "Joy in Item" the ballot calculates her "Joy in $100" (or vice versa).  It then apportions her money among her favorite items and these offers appear in the right- hand columns.  If one of her favorites is eliminated (by a mark under "Test Elim.") the ballot automatically transfers that money to lower choices.