|
Different uses for voting
need different types of voting. |
 |
Tally Options for
|
 |

DEMOCRATIC EVOLUTION OCCURING,
IMPROVING NEW RULES
|
|
|
Optimization, finding the best solution or at least improving on the initial solution, is far more important to voters in selecting projects than in electing reps. Elections offer voters several bundles of policies as embodied in the several candidates. The voters can’t choose one policy for each issue; they can hope to elect someone who will be good on most issues. (This is a strong argument for some forms of direct democracy and direct representation.)
But in selecting projects a voter can be precise, using his money only for his set of priorities. This page concerns theoretical/experimental issues for fair-share (FS) tallies, issues which probably interest professors and students, but not users. The MMV rules are still under development and so is this page. It is updated occasionally to refine ideas not style. Constructive criticism from readers is needed and welcomed. Suspend Weak CandidatesWhen there is no winner, just suspend or by-pass the item furthest from winning quota. In contrast, standard Instant Runoff Voting would eliminate the weakest item.For Suspension IRV, a ballot's single vote passes down the voter's list of choices, past candidates who have already been suspended and on to the highest choice in need of this vote. Any higher choice that has been suspended counts a Suspended Vote (SV) from this ballot. When an item is suspended, its offers are still offered but not reserved. If an item with suspended votes gets more offers later, it may yet get the quota needed to win funding. Here are four simple examples of one-seat and three-seat elections. In the one-seat elections, Suspended Votes elects the Condorcet Winner (CW) because it ends by comparing pairs. Here again is our example with 7 voters choosing 1 winner from 4 candidates or proposals -- which are labeled A, B, C and D. In each step or row, the candidate who gets, say Jo’s ballot, is highlighted in yellow. Any suspended candidates ranked higher than that yellow candidate will be grayed.
In step 1 below, no one gets a majority. Candidates A and C each have only 1 ballot so they are tied for last. C ranks higher on most ballots, so in step 1 we eliminate A and move Uri's ballot to his next choice, B.

Candidate B is the first to win a majority. But as soon as D is suspended, another suspended candidate, C, wins votes from 4 ballots prior them to passing those votes to B. So C is reinstated. C then wins a majority and when B is suspended, no one wins a majority in suspended votes. So C is our winner by Runoff Without Elimination. Click a ballot (in Table I) to highlight the candidate totals (in Table II) which that ballot helps. Or click on a candidate's total (in Table II) to check which ballots (in Table I) add to it. Click here to reset the ballots and the Instant Runoff table. You can see that there is more than one majority even in this small group with 7 voters. Proposals B and C each win a majority; so it is not accurate to claim either of them wins the majority. You can see the same votes tallied by Condorcet’s Pairwise Tournament or normal Instant Runoff Voting. A change of one rank by Uri will show how manipulation may create a voting cycle.
Here are three candidates taking positions along the political spectrum.
Eliminate B, squeezed in the middle.
Suspended Votes elects the Condorcet Winner (CW) if there is one because it ends with a series of one-against-one comparisons. But if there is a voting cycle, the tally loops endlessly because every candidate has at least one rival who gets suspended votes from more than 50% of voters. So this is not a "Condorcet-completion" rule. It is harder to tally than the Pairwise table. Donald Davidson at the University of Michigan proposed instant Runoff voting Without Elimination (RWE). He hoped it could unite advocates of elimination IRV together with fans of Condorcet’s Pairwise criterion. But the IRV supporters doubted the public would accept RWE as readily as IRV. Suspended Votes can speed finding a CPO-STV set of winners or a close approximation. That is hardest to do when funding projects with a wide range of costs. Accurate Democracy has recommended project tallies using SVs since 1996. (Back then the site was hosted by AOL and called "Democracy Evolves".) PoliticalSim’s help files recommended SVs several years earlier.
Here is a very simple example showing some of the twists and turns a SV tally can take. Both tallies have 40 voters electing 3 reps so the Droop quota is 11 votes. For simplicity, 2 candidates win on the first count.
Elimination STV elects A, E, B. Suspension STV elects A, E, C. This change saddens the 7 BC voters; but it pleases the 3 CB, 2 CD and 6 DC voters. So the affected voters prefer C to B by 11 to 7. Suspending offers leaves a ballot's weight pending for more items than it can afford. So after the first suspension, the tally can fund new winners only 1 at a time. Otherwise a ballot might spend its last weight on both reserved and (several) suspended items. (This is not an issue with Meek-style transferable votes.) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Table 5. Data for Charts 1 and 2 Vote Quota = 10
Item | Initial Ballot | 1. Utility Curve | 2. B Suspended
| Rank $Vote | Votes Offer | Votes Offer
A | 1 500 | 1.21 60.62 | 1.21 60.62
B | 2 500 | 0.68 33.85 | (0.68 33.85)
C | 3 125 | 0.44 5.53 | 0.7 8.75
D | 4 250 | 0 0 | 0.55 13.75
E | 5 250 | 0 0 | 0.5 12.50
|
![]()
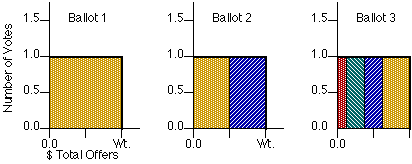

|
Charts 1 and 2 Suspension of B
Both charts show only the reserved offers. The offer for B is still made after suspension. It might be considered to be in the background of Chart 2, behind the other offers. Suspended votes are the votes a suspended item would get if it were reinstated. It is easiest to calculate them after the regular tally, reinstate all items that get a quota or more of suspended votes, and resume the tally. (A tally could reinstate 1 at a time, largest percentage over quota first, or reinstate suspended items as soon as they reach quota. But these options take longer to calculate and might create cycles.) Each of these paths can reduce the influence of the sequential order of suspensions. If formerly suspended items win, they must displace 1 or more previous winners. The notes on "delete last loser" and "sticky items" help show why this can result in a more intensely- or broadly-popular set of winners.
[ Ties[ Ties are uncommon when selecting the weakest item to suspend. That is because each voter's utility curve produces fractional votes. But there must be a rule for breaking the occasional tie. Here are 2 options; both find an item unlikely to get more offers. The quickest tallies a Condorcet Series before the MMV tally. This finds the Condorcet winner, the second best, and so on. Voting cycles are common when putting a list in order so Tideman’s Ranked Pairs rule is useful here. The tie-breaker suspends the least popular of the tied items.[ There is a more accurate way to find the item least likely to get more offers. Each ballot gets 10% more weight for a tie-breaker vote, 10% times weight not yet contributed (as though another top choice were suspended and its money could shift to a tied item). If that fails to break the tie, a larger percentage is used. (Allowing suspended votes to reinstate an item greatly reduces the importance of this tie breaking rule.) [ Ties are also uncommon among winners. Two or more may reach quota immediately after the suspension and transfer of money from another item. Again there are several ways to break ties. The best method funds the 1 which had the most initial offers. It has few offers transferred down from suspended items. If some items are still tied, use the ranks of items from the Condorcet Series. Fund whichever tied item was most popular according to Condorcet's rule. Very few ties will need to be broken randomly. (This is not an issue with Meek-style transferable votes.)
[ Collecting Contributions[ There are 4 basic ways to time the collection of contributions. The timing is likely to have some impact on utility but more on the equity of the results. It is most practical for now to use Meek-style transferable votes -- and to skip these 3 sections.[ a) Immediately collect contributions when the item reaches quota; then declare the item closed. Since these are the ballots that enthusiastically gave high ranks to that item, this way probably leads to a high average contribution and budget. If so, then few items will be funded. Also a few voters will contribute a lot of their weight to each winner, and each voter will help fund only a few items. [ The next 3 methods often lower item budgets because a voter who gives a low rank probably gives a low budget. They also catch free riders who rank sure losers as their top preferences -- so as not to spend weight on the early winners. [ b) Continue collecting offers made later to an item that has already reached quota and has taken contributions. Early contributors will get some weight back. (Recall that each voter's contribution was his preferred budget divided by the item’s actual number of contributors. If his budget is divided by a larger number of contributors, his contribution is smaller.) [ c) Delay collection until the end of the tally. Letting a ballot keep its weight till the end holds open its chance to fund a high-ranking suspended item, B, and drop lower-ranked winner G. But we know that several other ballots ranked G above B because G won before B did. (Or, if quota is proportional to cost and B costs more than G, we can say G has more contributors relative to cost than B does.) Letting B win must not cause G to lose. [ (This is similar to rules for STV transfers by Meek and by Warren. A key change: if there is money left over after 1 complete tally, MMV must revive suspended items which cost less than the amount leftover and which won their quota in suspended votes, then continue the tally.) [ d) Release frees offers reserved for sticky items. A "sticky" item can almost but not quite reach quota. A "stuck" ballot's weight remains reserved for such an item. The item gets eliminated late in the tally. But by then many of the ballot's other top preferences have also been eliminated. So some of the voter's weight goes to a very low preference or is not spent at all. The tally is run again and releases votes reserved for sticky items (previous losers) 1 item at a time. This might be called delete last loser. [ Each loser may yet win, but the voter's weight also may help his other top choices. When a ballot's losing votes all have been released, its weight is all reserved for winners of the previous tally or contributed to new winners. When no weight is reserved for losers on any ballot, then winners of the previous tally may win. The process may be repeated until the list of winners is the same for 2 consecutive tallies. But it does not always resolve; it may lead to a cycle. [ Like collecting late offers, this process catches free riders. Collecting late offers is easier to explain but releasing losers might be faster or more fair. They can work together. Exhausted ballotsA ballot is "exhausted" if it has money left but all of the items rated by the voter have won or been suspended. This leftover or "wasted" money can serve the organization's members by going to other ballots, to investment or emergency funds or to all ballots in the next funding vote.(It might help to tag an exhausted ballot as such, then make it give the MaxVote to any preference that wins. [But do not give MaxVote before an item wins; that would create an incentive for bullet voting.] This follows Newbury and Britton's 1973 method for using up weight from exhausted ballots under STV.) Labor HoursThe Voting Options page gave several ways to deal with projects which have more than one limiting resource such as money and labor. The advanced ballot allows another, more complex way.C) Link the money and labor tallies. Say a first-choice project, A, needs no hours, so it uses no space under the hours curve. The second-choice project, B, then is at the high end of the hours curve and could get a high labor vote, more than 1 offer. But let's say the first choice uses a lot of the money curve; so the second choice is not high on the money curve. It might not get even 1 vote according to its area under that curve. We must use the smaller of the two votes. In this case the money vote for B times 1 offer of hours will limit its area and width on the hours curve, even though it is at the tall side of that curve. This ballot is likely to end up with surplus hours. But it still could give a large vote to a project which needs little or no money, just a lot of hours. Ballots which lack money or hours may join resource pools which trade money for hours at a pre-set rate, say $20 an hour. Even with pools to exchange resources, one will run out before the other. ConclusionThis chapter presents 4 or 5 important innovations for Movable Money Votes:1) Allocate some funds by a central rule before a fair-share rule. 2) Combine a ballot quota and a cost quota into a contribution quota. 3) Distribute each ballot's money according to its own utility function. 4) Check suspended votes for potential winners [or delete last losers]. 5) Protecting higher choices may be important to some voters. At least 2 innovations need more development:
|

|
|




 Accurate Democracy
Accurate Democracy