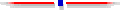|
Different uses for voting
need different types of voting. |
 |
Limited Vote for Projects |
 |

Notes on refining the project funding rules in one community.
Many people understand an innovation's importance and operation quickly if they read the history of its development.
The Current RuleWhen you give money to an item, 1 vote is added to it's vote total. The items with the most votes win. Your budget for the item is added to its dollar total. That is divided by its vote total and this average dollar amount becomes its budget.B. Every item you vote for gets 1 vote. Your first choice gets no more than the last choice in your budget. The tally is as likely to fund bottom choices as top choices. A Simple ChangeWe can make the current rule simpler for the community's voters (they won't have to repeatedly add a long column of large numbers) and make it pick more desirable projects (pro-jects that are highest priorities for more voters).You still write budget amounts beside your favorite items. But you do not need to keep adding up the total. In-stead, rank the items as first choice, second choice, third and so on. The people and software that count the votes will give 1 vote to all of your favorite items that fit in the budget. If your ballot has some money left, but only half the amount you wrote for the next item, it gets a half vote and the rest of your ballot's money. Your vote is added to the item's vote total, and your dollars to its dollar total. Its dollar total is divided by its vote total and this average dollar amount becomes the item's budg-et. A Further ChangeWould you like to give more than 1 vote to your top priori-ty, even if you would have to give less than 1 vote to your last priority? We can do that but we should avoid 2 errors.It is widely known that the best strategy for point voting is to dump all of your votes on your favorite. This is bad for decision making. It is not an accurate or sincere vote. It doesn't tell the community or the voting rule how one feels about any other items. It rewards exaggeration. So there should be an upper limit: perhaps one and a half votes for first choice, 1 vote for a middle choice, and a half vote for last item in your budget. The second error would be to give 1.5 votes to any first choice, regardless of cost -- that would lead to everyone ranking expensive items at number 1. The first dollar allocated by a ballot gets 1.5 votes. The last dollar gets only 0.5. The average dollar's value as a vote is 1. An item gets a vote equal to the average value of its dollars. These limitations form the basis of the Limited Utility Rule (LUR). For visual thinkers: In these graphs, column widths show costs of items; heights show votes for items. The new rule gives this ballot's first item a vote of 1.4. A first choice that cost twice as much would add lower utility dollars. Its average utility would be about 1.3.
The 2 graphs above are straight-line utility func-tions. Most social scientists would not hazard to guess the most common shape for personal utility curves. Most who do guess say a square root curve fits best. Free LUR ballot and tally templates available below include both straight-line and square-root functions. A voter may score items instead of rank-ing them. His scores may tell either Util D, the joy he expects from each dollar spent on the item, or Util I, his total joy from the item, in which case the score is divided by the cost to give Util D. Scores let the voter create the ballot's utility curve; preferences are not forced to fit a shape such as the graphs above. The area under each ballot's utility curve is still 1 vote times 1 ballot weight. Its average vote will be 1, but the first item's dollars might be worth up to [2] votes while the value of the last item's may be much less depending on the voter's scores for the items. These scores primarily compare utility values be-tween items on a person's ballot, not between ballots. Unfor-tunately, scores may lead some voters to waste time worrying over their ballots. There are no "correct" answers; self-expression, not precision, is the mode of thinking while voting. Scores are harder to type in than ranks, but easier than preferred budgets. The planners can run simple variations to create 3 sets of winners. One variation is the rule used for past OTRAs. The most popular items will be winners in all sets. But 1 set will emphasize broad popularity, the other sets will include items with fewer but more enthusiastic supporters. Members then discuss the consequences of this set versus that and vote on which is the best package. To understand the variations, it will help to under-stand 2 election rules: bloc vote and limited vote. Both are used in at-large elections, for example, a five-seat city council in which all candidates compete in one, city-wide district. A voter may give only 1 vote to a candidate. The 5 candidates who get the most votes win. Bloc vote lets a voter cast as many votes as there are seats to fill (or as many dollars as there are to spend). A majority group with 5 candidates for 5 seats wins all 5. No other candidate can win more votes. (This is why federal judg-es in several jurisdictions have found that bloc vote has denied minorities representation and so is illegal under the Voting Rights Act.) Past OTRAs have used this rule and it still will be one variation. Limited vote lets a voter cast fewer votes (or fewer dollars). Each voter in a five-seat district might cast 3 votes. If the majority gave all its votes to 3 candidates they would win those 3 seats a majority -- but not all of the seats. This is why limited vote usually results in fairer, more equal representation than bloc vote. EliminationIf a group's votes are divided evenly among too many can-didates, most of them lose. The majority of voters could get less than a majority of the reps (or OTRA dollars). Bloc vote fails to transfer a ballot's vote from a hopeless candidate with few supporters, to the ballot's lower-ranked but more broadly-popular candidates. Like STV and TAS, the Limited Utility Rule avoids this pitfall by allowing elimination the weakest candidates, 1 at a time. But LUR is not as good at transferring excess votes from a winner.Perhaps the voter's ballot should show him utility-scaled scores for more than the limited budget. Some of his favorites will be eliminated. His utility points would transfer to lower choices and he needs to see relative scores for those choices.
Simple spreadsheets for LUR may be downloaded here. Each set includes a ballot and a tally sheet.
Links to the 1998 edition. |

|
|



 Accurate Democracy
Accurate Democracy